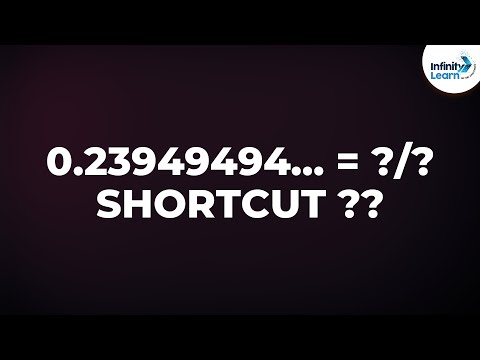Why Form 8854 Termination 2023-2024

You solved for sums in the previous two parts and got the following answers: - 0.3 with a bar over 3 as 3/9 - 0.75 with a bar over 5 as 68/90 - 0.352 with a bar over 352 as 352/999 - 0.2394 with a bar over 94 as 2371/9900 - What you did was convert the decimals to rational number form P/Q, but the procedure used was very long and arduous, which made it time-consuming and boring. Let's look at a shortcut, a quicker way to solve it. - First, let's classify the decimal numbers into simple or mixed recurring decimal numbers. - The first decimal is simple since all the digits after the decimal point are repeated. Even this number is simple since 352 is repeated after the decimal point. They are also called pure recurring decimals. - In the second example, the bar lies above the number 5 and the digit 7 is not repeated, so it's a mixed recurring decimal. - In this example, only 94 is repeated and not 23, so it's a mixed decimal too. - Now let's focus on the simple decimals. Do not look at the answer for now. - The denominator of the fraction will have as many nines as the number of recurring digits. Here we have just one recurring digit, so the denominator will be 9, and the numerator is 3. That's your answer. No equations, no subtraction, no variables, nothing. - Let's understand it with another simple recurring decimal. - The denominator will contain as many nines as the number of recurring digits. Here we have three recurring digits (352), so we will have 999 in the denominator, and the numerator is 352. That's your answer: 352/999. - Remember, for simple decimal numbers, the denominator will have as many nines as the number of recurring digits, and the numerator is written without...